Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
molekulová fyzika
6. Série 10. Ročníku - 1. kapalina mezi rovnoběžnými deskami
Odvoďte vztah pro výšku $h$ hladiny kapaliny mezi dvěma svislými nekonečně dlouhými rovinami, vzdálenými od sebe $d$, které jsou ponořeny do kapaliny. Povrchové napětí kapaliny je $σ$ a hustota je $ρ$.
3. Série 10. Ročníku - 4. cirkus
Artista padá na silně napnutou plachtu z výšky $h=1\;\mathrm{m}$. Jaký bude maximální průhyb plachty, je-li průhyb s artistou v klidu $Δy=2\;\mathrm{cm}?$ Považujte všechny výchylky za malé.
2. Série 10. Ročníku - 3. jarový tryskáč

Matouš si vystřihl z tvrdého papíru lodičku, která je nakreslena na obr. 3 při pohledu shora. Do místa $A$ pak kápl kapičku jaru a loď spustil na vodní hladinu. Nemálo se podivil, když loď sama od sebe vyrazila prudce vpřed. Umíte pohyb lodi vysvětlit? Platí pro něj zákon zachováni energie?
1. Série 10. Ročníku - P. balónek
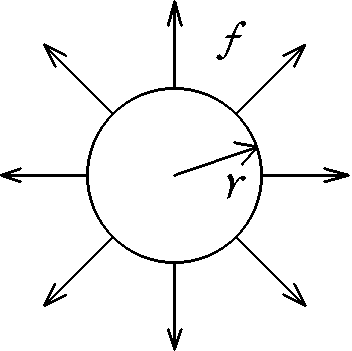
Jak moc můžete nafouknout pouťový balónek, dokud nepraskne? Předpokládejte, že balónek má tvar koule. Nenafouknutý nechť má poloměr $r_{0}$. Je z gumové blány, která má v přiblížení následující elastické vlastnosti.
Roztahujeme-li kruh vyříznutý z této blány na okraji tak, že síla na jednotku délky obvodu je $f$, bude poloměr kruhu $r$ přímo úměrný $f$, $r=r_{0}(1+af)$, $a$ je konstanta úměrnosti (viz obrázek). Materiál praskne při maximální síle na jednotku délky $f_{max}$. Na jedno nadechnutí naberete do plic objem $V_{fuk}$ vzduchu a ten pak fouknete do balónku. Kolikrát můžete do balónku fouknout, než praskne, a jaký bude mít rozměr?
3. Série 8. Ročníku - E. grant strýčka Skrblíka
Vašim milovaným strýčkem vám byl zadán úkol zjistit, zda jeho památeční rodinná lžička jest skutečně z ryzího hliníku. Vaše experimentální vybavení je však poněkud skromné: kromě uvedené lžíce dostanete k dispozici závaží o známé hmotnosti, dlouhé pravítko, provázek a dva hřebíky, které můžete zatlouct do zárubně dveří. Navíc zde ještě stojí kbelík plný vody. Navrhněte, výpočty podložte a hlavně proveďte měření, při kterém co nejpřesněji s pomocí jmenovaných pomůcek určíte hustotu materiálu lžičky. Uskutečněte dostatečné množství měření a na základě alespoň nějakých kalkulací také odhadněte věrohodnost vámi obdrženého výsledku.
Nápověda: Pokuste se srovnat hmotnost lžíce a závaží zavěšováním na provázek, který jste (s mírným průvisem) natáhli mezi zárubní dveří.
1. Série 8. Ročníku - 3. disk
Franta vytáhl dva stejné skleněné disky o průměru $10\; \textrm{cm}$ a tloušťce $4\; \textrm{cm}$ z vodní lázně a přiložil je k sobě (souose) jejich zcela vyhlazenými podstavami. Mezi nimi zůstane souvislá vrstvička vody o tloušťce $0.5\; \textrm{mm}$. Odhadněte (alespoň řádově) velikost síly, jakou musí vynaložit na odtržení disků od sebe, působí-li kolmo na jejich podstavy.
Poté disky osušil a znovu přiložil k sobě, přičemž k jejich dokonalému přilnutí mezi ně vložil list velmi tenkého hedvábného papíru. Jakou silou je potřeba působit nyní?
1. Série 8. Ročníku - E. bungee-jumping
Zajisté jste slyšeli o novém druhu zábavy lidí, kteří si potřebují dokázat, jak snadné je překonat vlastní strach. Z vlastní vůle skočit z výšky třeba $50\; \textrm{m}$ přivázán jen za nohy, není to lákavé? Vaším úkolem by mělo být: laboratorně zkoumat dynamiku tohoto nového sportu (kdy se asi dostane do olympijských her?) a na základě pokusů domácky provedených učinit závěry z toho plynoucí pro člověka přivázaného na takovém laně.
Nejprve si obstaráte kus gumy přiměřené délky. Pak můžete měřit:
- závislost maximální hloubky $h$ na délce gumy $l$, do níž se závaží hmotnosti $m$ klesne
- závislost hloubky $h$ na hmotnosti závaží $m$ pro dvě různé délky gumy $l_{1}$, $l_{2}$. Pozor abyste nepřekročili kritickou hmotnost $M_{K}$ z bodu $c$!
- jaká je kritická hmotnost $M_{K}$ závaží, při němž se guma délky $l$ přetrhne (tento úkol předpokládá, že máte dost experimentálního materiálu a máte též vhodnou gumu – zachovává pružné vlastnosti až do přetržení)
Pro člověka vysícího na takovém laně má značný význam maximální zrychlení na něj působící po čas letu. Pokuste se toto zrychlení určit na základě změřených výsledků.
Přejeme Vám mnoho úspěchů při řešení a hodně zábavy s praskající gumičkou!
3. Série 7. Ročníku - 4. velikost atomu
Odhadněte velikost atomu, resp. molekuly látky, znáte-li koeficient povrchového napětí, hustotu a měrné výparné teplo. Porovnejte s tabelovanými hodnotami, např. pro rtuť či vodu.
1. Série 2. Ročníku - S. zeměměřiči
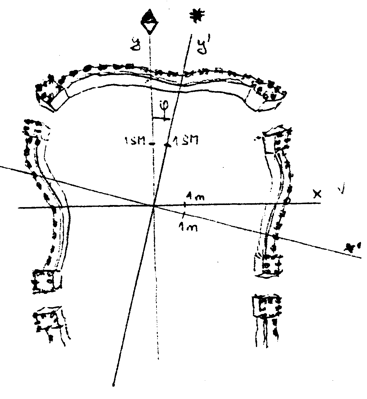
Za devatero horami v Severním království pod vládou moudrého krále žijí dva národy – denní a noční lidé. Pro potřeby obou národů zde pracují dva velcí zeměměřiči. Denní zeměměřič měří vzdálenosti k východu od středu náměstí hlavního města v metrech (označme $x$) a vzdálenosti v severním směru, který je zde považován za posvátný, měří v severských mílích ($y$). Sever určuje podle magnetky kompasu. Noční zeměměřič určuje sever podle Polárky a vzdálenosti od středu náměstí k východu opět měří v metrech ($x′$) a k severu v severských mílích ($y′$). Jednoho dne chtěli porovnat své výsledky. Ocitli se však před velkým problémem. Vzhledem k tomu, že směr k Polárce není shodný se směrem k magnetickému pólu, tak se jejich údaje liší.
- Pomozte jim a odvoďte vztahy mezi údaji $x$, $y$ a $x′$, $y′$.
- Jak by vztahy mezi $x$, $y$ a $x′$, $y′$ vypadaly, kdyby oba zeměměřiči neměřili vzdálenosti ze stejného místa?
2. Série 1. Ročníku - P. balónek
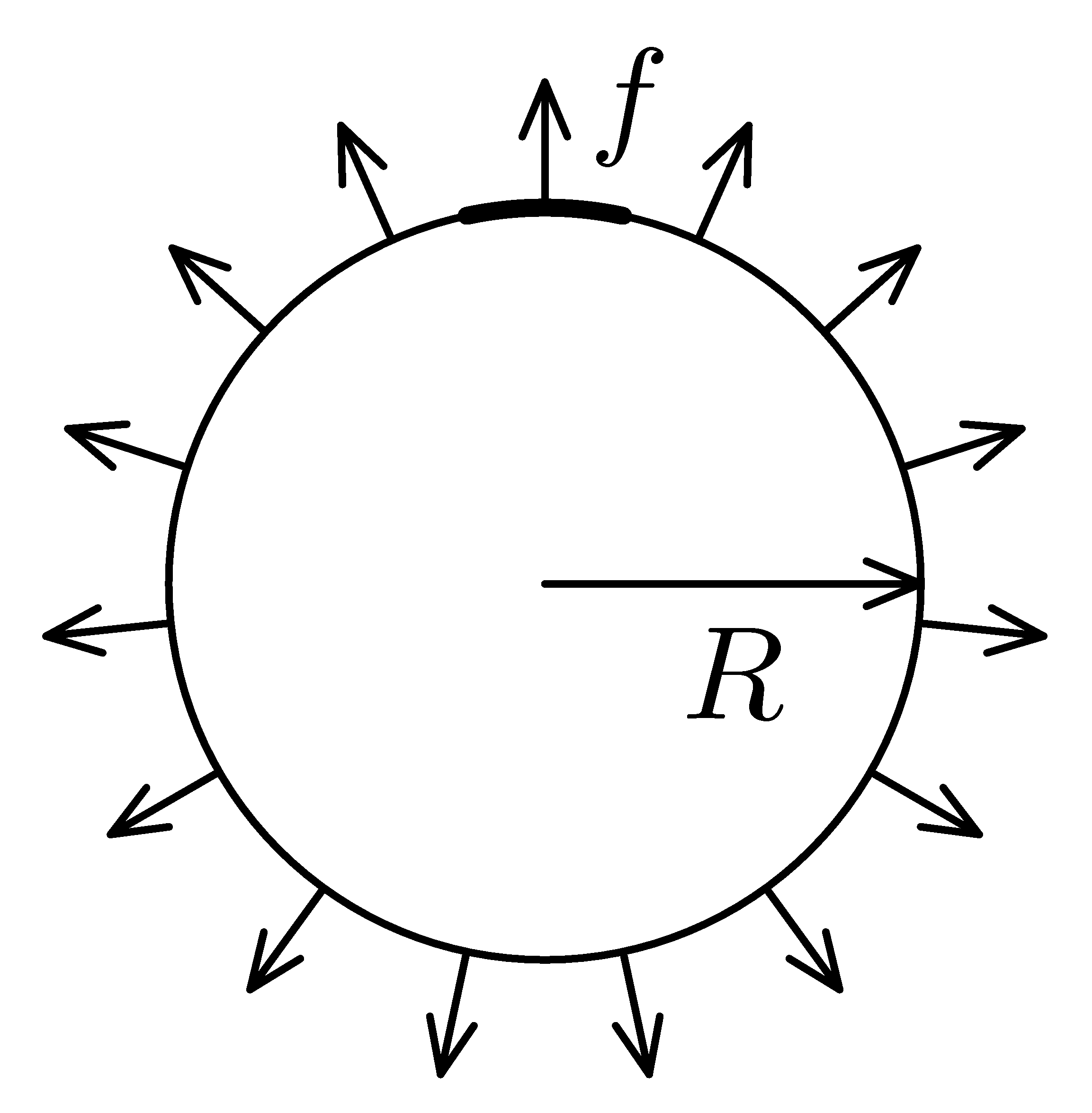
Model balónku
Jak moc můžete nafouknout pouťový balónek, než praskne? Předpokládejme, že balónek má tvar koule. V nenafouknutém (nebo velmi slabě nafouknutém) stavu nechť má poloměr $r_{0}$ (třeba $5\; \textrm{cm}$). Je z gumové blány, jejíž elastické vlastnosti i pevnost známe. Na obrázku je znázorněn kruh vystřižený z materiálu, z něhož je balónek. Tučně vyznačená délka obvodu je jednotková. Pro jednoduchost předpokládejme, že kdybychom kruh z této blány roztahovali na okraji (viz obrázek) tak, že by síla na jednotku délky obvodu kruhu byla $f$, byl by poloměr kruhu přímo úměrný $f$.
$R=R_{0}(1+αf)$. Maximální síla na jednotku délky (při níž materiál balónku praskne) nechť je $f_{max}$.
Předpokládejme dále, že na jedno nadechnutí naberete do plic objem $V_{fuk}$ vzduchu a ten pak fouknete do balónku. Kolikrát můžete do balónku fouknout, než praskne, a jaký bude mít rozměr? (Zkuste též odhadnout reálné hodnoty veličin v problému vystupujících a diskutovat oprávněnost předpokladů.)