Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
mechanika tuhého tělesa
1. Série 11. Ročníku - 2. zlaté sloupy
Dva identické zlaté sloupy výšky $200 \,\jd{m}$ a průřezu $1 \,\jd{dm^2}$ jsou umístěny vedle sebe. Jeden z nich je zavěšený a druhý stojí na podložce, oba mají stejnou teplotu $0 \,\C$. Oběma dodáme teplo $5\cdot 10^{6}\, \jd{kJ}$. Budou mít potom stejnou teplotu? Jestliže ne, odhadněte, o kolik se jejich teplota bude lišit. Potřebné údaje si najděte v tabulkách, tepelnou výměnu s okolím zanedbejte.
1. Série 11. Ročníku - 3. slepičí problém
Slepice se po obědě (12:00) chce dostat do kurníku. Neumí však létat, a jelikož žebřík po stěně kurníku klouže, začne bezradně běhat kolem něj. V kolik hodin se do kurníku dostane, když každou hodinu běhání shodí $40\,\jd{g}$ a ve 14 hodin hodlá snést vajíčko? Ve 12:00 váží slepice $m=1,7\;\mathrm{kg}$, vajíčko má hmotnost $m_{v}=30\,\jd{g}$ a žebřík $M=5\;\mathrm{kg}$. Výška kurníku nad dvorkem je $h=0,85\;\mathrm{m}$, sklon žebříku $α=25°$, součinitel smykového tření mezi kurníkem a žebříkem i mezi dvorkem a žebříkem je stejný: $f=0,7$.
1. Série 11. Ročníku - 4. grant strýčka Skrblíka
Zlepsovak 1
Strýček Skrblík se jednou doslechl o perpetuech mobile a vytušil příležitost, jak ještě více zbohatnout. Vypsal grant na vymýšlení „věčných strojů“, ale jediní, kdo se přihlásili, byli jeho synovci. Přinesli strýčkovi následující tři nápady:
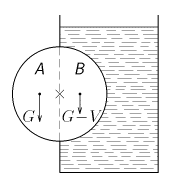
- Základem prvního perpetua je válec, který je dutý, vodotěsný a je upevněn v ose na valivých ložiscích. Obrázek nám objasní funkčnost stroje. Na obě části válce sice působí tíhová síla $G$, ale část $B$ je vůči části $A$ válce nadlehčována vztlakovou silou $V$ dle Archimédova zákona. Válec se bude otáčet a jeho rotační energii převedeme na elektrickou energii.
- Pokud zahřejeme kapalinu, zvětší svůj objem. Zároveň víme, že kapalina je nestlačitelná. Proto budeme kapalinu zahřívat a ochlazovat, změnu jejího objemu převedeme na mechanickou energii a tu na energii elektrickou. Část takto obdržené energie využijeme na zahřívání kapaliny (ochlazení kapaliny zajistí okolní prostředí, odborně „lázeň“). Zbytek energie roztočí stroje ve Skrblíkových továrnách.
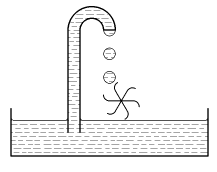
* Do nádoby s vodou je zasunuta kapilára. Díky kapilárním jevům voda naplní celou kapiláru a z horního zahnutého konce odkapává dolů, jak je to vidět na obrázku. Dole je umístěna vodní turbína, která je roztáčena padající vodou, a tak může konat práci.
Strýček se nadšeně pustil do výroby těchto strojů, jaké však bylo jeho zklamání, když zjistil, že ani jediný z nich nefunguje. Od té doby už o žádných „perpetech“ nechce ani slyšet.
Na vás teď je, drazí řešitelé, abyste se pokusili vysvětlit, proč žádný z nápadů synovců strýčka Skrblíka nemůže fungovat jako perpetuum mobile.
6. Série 10. Ročníku - 2. pružina, kvádr a tření
Na obrázku máme dva stejné kvádry o hmotnosti $m$ spojené pružinou o tuhosti $k$. Koeficient tření (klidového i smykového) je $f$. Jakou minimální rychlostí $v$ musíme poslat kvádr č. 2 směrem ke stěně, aby se v průběhu nastalého děje pohnul i kvádr č. 1?
6. Série 10. Ročníku - 3. kulečník
Máme $N$ identických kulečníkových koulí, které leží na nekonečně velkém, ideálně rovném a vodorovném kulečníkovém stole. Jednu kouli uvedeme do pohybu. Po jistém počtu nárazů se koule vrátí zpět a zůstane stát. Jaký je minimální počet koulí, aby to bylo možné. Všechny rázy jsou dokonale elastické.
5. Série 10. Ročníku - 1. rozmazaný šroub
Po nakloněné rovině se sklonem $β$ se z klidové pozice valí válec, na kterém je předkreslen závit. Válec se stále zrychluje a postupně se nám jednotlivé závity „rozmažou“, až není poznat, že tam jednotlivé závity byly. Měříme čas od puštění válce do chvíle, kdy nerozeznáme jednotlivé závity. Jak tento čas závisí na úhlu $β?$ Předpokládejte, že oko má snímkovací frekvenci $f$, válec má průměr $R$, stoupání závitů je $s$.
5. Série 10. Ročníku - 2. vykradená pyramida
Jistý duševně chorý faraon si před mnoha tisíci lety nechal vytesat mnoha tisíci otroků z jednoho kusu mohutné skály pyramidu. Starověcí zloději o dvě dynastie později chtěli pyramidu vyloupit, leč nenašli vchod, a tak se rozhodli, že se pokusí pyramidu převrhnout. Do její špičky zaklesli pevný kruh, jímž provlékli ještě pevnější lano. Za lano pak zapřáhli organizovanou skupinu otroků táhnoucích směrem od pyramidy kolmo ke dvěma hranám podstavy (obr. 1). Podaří se otrokům pyramidu převrhnout, když jich bude dostatečně mnoho, nebo ji po písku jen kus popotáhnou? Okolní písek je dokonale udusán minulými generacemi vykradačů hrobek, kteří už celá staletí obhlíželi, kudy pyramidu vykrást, takže se pyramida do písku nebude bořit. Hmotnost pyramidy je $M$, koeficient statického smykového tření je $μ$. Pyramidu považujte za jehlan (pohřební dutina je velmi malá, protože vládce je celý seschlý).
5. Série 10. Ročníku - 3. velké válení
Mějme dva duté válce vnějších poloměrů $R_{1}$, $R_{2}$ a vnitřních poloměrů $r_{1}$, $r_{2}$ ($r_{2}<R_{2}<r_{1}<R_{1})$. Válce jsou vloženy do sebe (obr. 2) a navzájem se po sobě valí, ale nekloužou. Vnější válec se začne valit po nakloněné rovině s úhlem $α$. Jakého zrychlení celá soustava dosáhne? Nad rámec zadání se můžete pokusit popsat pohyb jednotlivých válců. Hmotnosti válců jsou $M_{1}$, $M_{2}$ a materiál válce můžeme považovat za homogenní. Změní se řešení výrazně pro tři válce?
5. Série 10. Ročníku - P. šlechtic
Veliký šéf semináře radostně přeskakuje fluktuace hmoty ve svém pokoji B609. Právě dopadl plnou vahou z výše $H=1\;\mathrm{m}$ nad zemí volným pádem na hrábě. Násada je dlouhá $l=2,0\;\mathrm{m}$ a váží $m_{2}=1\;\mathrm{kg}$, část ocelového hrabla kolmá k násadě je dlouhá $z=7\;\mathrm{cm}$ a váží $m_{1}=2,5\;\mathrm{kg}$ (považujte jej za homogenní). Jakou rychlost má konec násady hrabí v okamžiku, kdy se opovážlivě dotkne nosu našeho nejvyššího? Srážku považujte za nepružnou. Šéfův nos se nachází $180\, \jd{cm}$ nad podlahou, šéfova hmotnost činí $92\, \jd{kg}$ včetně klíčů v pravé kapse.
1. Série 10. Ročníku - 1. stojánek na víno

Firma Strýček Skrblík s. r. o. zaplavila domací i zahraniční trhy geniálním výrobkem – dřevěným stojánkem na víno, jehož podobu si můžete prohlédnout na obrázku. Bude tento stojánek funkční? Závisí stabilita systému stojánek–láhev vína na velikosti a tvaru láhve či na množství moku v láhvi obsaženém? A pokud ano, tak jak?