Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (70)elektrický proud (75)gravitační pole (80)hydromechanika (146)jaderná fyzika (44)kmitání (56)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (295)mechanika plynů (87)mechanika tuhého tělesa (220)molekulová fyzika (71)geometrická optika (77)vlnová optika (65)ostatní (164)relativistická fyzika (37)statistická fyzika (21)termodynamika (153)vlnění (51)
mechanika hmotného bodu
2. Série 2. Ročníku - E. homole
Sypeme-li přášek (suchý písek, mouku apod.) volně na jedno místo, vznikne kužel s vrcholovým úhlem $α$. Co lze o tomto úhlu pokusně zjistit? Umíte výsledek nějak zdůvodnit?
1. Série 2. Ročníku - 1. člověk na voru
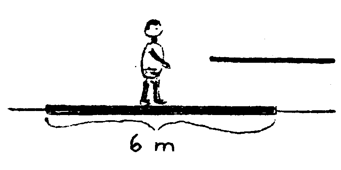
Člověk stojí uprostřed voru na vodní hladině a v určité vzdálenosti je tyč, kterou chce chytit. Jak daleko může být tyč, aby k ní po voru mohl dojít? Zanedbejte nejdříve tření mezi vorem a vodou. Jak se situace změní bez tohoto předpokladu? Hmotnost člověka je $75\; \textrm{kg}$, hmotnost voru $50\; \textrm{kg}$.
1. Série 2. Ročníku - 2. Ptolemaios a Koperník
Vraťme se ke středověkému sporu. Roku 1543 ve svém díle De Revolutionibus orbium coelestium Mikuláš Koperník předkládá svůj heliocentrický výklad světa, kterým popírá zažitou geocentrickou představu zformulovanou nejjasněji Ptolemaiem v díle Megalé Syntaxis v 2. století n. l. Umožněme myšlenkově oběma astronomům setkání, na kterém by mohli obhajovat svůj názor.
Koperník: „V mém výkladu je Slunce nepohyblivé a kolem něj se pohybují všechny planety včetně Země po kruhových drahách, což je mnohem jednodušší než popis pohybu planet v geocentrické představě.“ (Eliptické dráhy přinesl až o 60 let později Kepler.)
Co na to Ptolemaios? Kdyby byl hodně chytrý, odpověděl by třeba toto: „Tvůj názor je odvážný, mladíku, (Koperník byl o 1400 let mladší), ale myslím, že nepřináší nic nového, jenom zmatek v ustálených představách. I kdyby podle Tebe Země obíhala kolem Slunce, když se postavíme na Zemi, což stále děláme, uvidíme, že Slunce se pohybuje relativně vůči Zemi a to po kružnici. Pohyb je relativní!“ (Vskutku, pokud se nám pohyb jednoho tělesa z druhého zdá kruhový, tak opačně z prvního se pohyb druhého bude zdát opět kruhový – ověřte si to.) „Zapomeňme třeba na ostatní planety a mějme jen Slunce a Zemi. Můžeš i pak tvrdit, že Země obíhá kolem Slunce a ne naopak?“
Koperník: „Ano, i pak. Slunce stojí vůči stálicím, vůči hvězdám, a Země ne.“
Ptolemaios: „A proč by se stálice také nemohly pohybovat kolem Země? Copak Země středem vesmíru není lákavá myšlenka?“
Vidíme, že pan Koperník se dostává do úzkých. Vždyť Ptolemaios argumentuje tak revolučními a přitažlivými myšlenkami, jako že pohyb je relativní. My bychom se však přiklonili spíš ke Koperníkovi. Máme proti němu ale výhodu – víme, s čím přišel o necelých 150 let později pan Newton. Přizvěme ho k debatě. Jakými slovy vyřeší spor obou astronomů a přesvědčí Ptolemaia, zatím ale neřekneme. Co byste na místě Newtona řekli vy?
1. Série 2. Ročníku - 3. držák
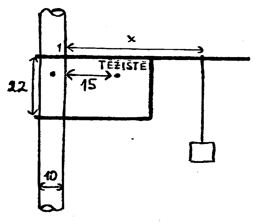
Držák na zavěšení lehkých břemen, který lze lehce připevnit v libovolné výšce, je často velmi praktický. Jeden takový držák je na obrázku i s rozměry. Může se vertikálně posunovat po tyči a udržuje se v určité úrovni silou tření. Koeficient statického tření mezi držákem a tyčí je $0,30$, tíha závaží zavěšeného ve vzdálenosti $x$ od tyče je $50$krát větší než tíha držáku. Jaká je minimální hodnota $x$, při které držák ještě nesklouzne dolů?
4. Série 1. Ročníku - 4. netradiční ohřívání čaje
Kolik nábojů je zapotřebí k uvaření šálku čaje? K dispozici máte ocelovou polní konvičku o hmotnosti $4\; \textrm{kg}$ a samopal. Náboje mají hmotnost $16\; \textrm{g}$ a rychlost $700\; \textrm{m}\cdot \textrm{s}^{ -1}$.
3. Série 1. Ročníku - 1. film
Filmový pás zachycuje padající těleso se zrychlením směrem dolů. Pustíme-li film pozpátku, bude mít zrychlení tělesa směr
- nahoru
- dolů
Zdůvodněte.
3. Série 1. Ročníku - 2. planeta liliputánů
Představte si, že do rána se všechny vzdálenosti a rozměry předmětů zvětší desetkrát, přičemž jejich hmotnost se nezmění. Jaké by byly důsledky?
3. Série 1. Ročníku - 3. tramvaj
Ve stojící tramvaji visí u svislé desky na niti délky $l$ citrón o hmotnosti $m$ (předpokládáme, že rozměry citrónu jsou velmi malé v porovnání s délkou niti). Tramvaj se rozjede se zrychlením $a$, které můžeme považovat za konstantní. Spočtěte, kam až toto kyvadlo vykývne (jaký maximální úhel bude svítat s deskou) a kdy citrón opět ťukne do desky.
3. Série 1. Ročníku - E. přetahovaná
Na kulatý sloup či tyč je namotáno několik závitů lana. Z jedné strany drží lano třeba malé dítě a táhne za něj malou silou $F_{d}$ (třeba $1\; \textrm{N}$). Z druhé strany táhne za lano obr. Jak velkou silou může obr za lano táhnout, aniž by dítě na druhém konci „přetáhl“? Předpokládáme, že sloup se nemůže otáčet.
Zkuste výsledek odvodit teoreticky, ale zejména vyšetřete daný problém experimentálně. (Jaká je závislost síly na materiálech sloupu a lana, velikosti sloupu, počtu závitů – a má např. smysl „neceločíselný“ počet závitů? Atd., atd. Obra i dítě můžete nahradit jinými pomůckami, sloup také.)
2. Série 1. Ročníku - 1. silák
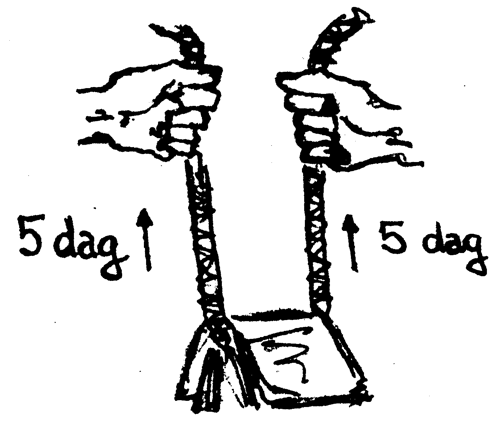
Uvolněné lano

Vodorovně napnuté lano
Za devatero horami je země, v níž se síla měří v jednotkách zvaných $\textrm{dag}$. Na pouti tam silák napíná oběma rukama lano, na němž je zavěšen telefonní seznam o tíze $10\; \textrm{dagů}$. (Kdyby silák držel oba konce provazu u sebe, napětí v obou částech lana by bylo $5\; \textrm{dagů}$.) Jaké bude napětí v obou částech lana, když silák roztáhne lano do vodorovné polohy?
- $5\; \textrm{dagů}$
- $10\; \textrm{dagů}$
- $20\; \textrm{dagů}$
- více než milión $\textrm{dagů}$