Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
matematika
6. Série 8. Ročníku - S. hledání kořenů polynomu
Napište (a zašlete) program, který určí všechny kořeny polynomu. S jeho pomocí nalezněte čtyři řešení rovnice $x^{4}+2x^{3}+5x^{2}–4x+3=0$.
5. Série 8. Ročníku - 2. obvod bez zdrojů
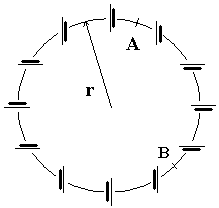
Mějme velmi jednoduchý obvod složený ze $n$ stejných ideálních zdrojů o napětí $U_{e}$ sériově zapojených do kruhu o poloměru $r$. Dráty je spojující mají stejnou délku a měrný odpor $ρ$ na jednotku délky (rozměry zdrojů zanedbejte vůči obvodu kružnice). Jaké bude napětí mezi bodem $A$ uprostřed prvního a $B$ uprostřed $k$-tého drátu?
Na obrázku je nakresleno zapojení konkrétně pro $n=12$ a $k=5$.
5. Série 8. Ročníku - S. obyčejná
Sestavte program pro iterační metodu a zvolte vhodnou konstantu $k$ pro fci $g$, abyste dostali vhodný interval okolo 1 splňující kontraktivnost. Ověřte lineární konvergenci a zkuste zjistit míru zrychlení při užití Aitkinova procesu.
4. Série 8. Ročníku - S. tečná metoda
Vezměte poslední popisovanou metodu tečen neboli Newtonovu, která určuje následující bod podle vzorce $c=b-\frac{\textrm{funkce}(b)}{\textrm{derivace}(b)}$ – pro ty neznalé derivování uvádíme pro náš případ
$$\textrm{derivace}(t)=-gt+v-\frac{2pA}{T}\sin\left(\frac{2pt}{T}\right)$$
Řešte touto metodou zadanou úlohu a ověřte rychlost konvergence jak pro přesný odhad počátečního intervalu $(0,88;\; 1,02)$, tak pro hrubý odhad $(0;\; 10)$.
Zjistěte, jak závisí přesnost dosaženého výsledku na počtu kroků u všech popsaných metod (bisekce, regula falsi, metoda sečen a tečen), tedy ověřte, zda je zpřesňování lineární, kvadratické, či jiné. Je tato vlastnost ovlivněna volbou počátečního intervalu?
3. Série 8. Ročníku - 4. odpor 4-rozměrné krychle
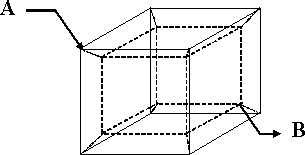
Model 4-rozměrné krychle
Představte si krychli ve čtyřrozměrném prostoru, jejíž hrany jsou tvořeny odpory $R$ (pomůckou vám bude obrázek, který zachycuje ekvivalentní zapojení ve třech dimenzích znázorněné na dvourozměrném papíře). Vaším úkolem je spočítat výsledný odpor mezi body na tělesové úhlopříčce (mezi levým horním předním vnějším rohem na obrázku – bod $A$ a pravým dolním zadním vnitřním rohem – bod $B$). Zdá-li se vám to příliš snadné, pokuste se zobecnit výsledek pro libovolnou hodnotu dimenze $n$ (a případně určete k jaké hodnotě se jejich odpor blíží pro $n$ rostoucí k $∞$).
3. Série 8. Ročníku - S. trochu jiná metoda
Upravte program uvedený v minulé sérii z metody regula falsi na metodu sečen a zjistěte, jak se zrychlí konvergence metody na stejném příkladu jako v minulé sérii. Úlohu uvažujte čistě kinematicky, bez počítání hybností a sil: deska kmitá jako volný harmonický oscilátor a skokan se pohybuje jako hmotný bod ve svislém vrhu. Ověřte, jak mnoho je nyní konvergence závislá va volbě výchozího bodu. Pokuste se metodu zrychlit pomocí Aitkinova procesu: vždy po třech přiblíženích spočtených bežným způsobem proveďte extrapolaci k řešení $γ$. Jak se uvedený postup vyplatí při metodě regula falsi a při metodě sečen?
2. Série 8. Ročníku - 4. pavouk a moucha
Na povrchu skleněné koule je pavouk a moucha. Kde musí být moucha, aby ji pavouk uviděl? Počítejte s tím, že koule je větší než pavouk a moucha (dohromady), přičemž mnohokrát. Index lomu pro sklo je $1,43$.
1. Série 8. Ročníku - 2. Mňága a Žďorp
Mňága vyjíždí na kole rychlostí $15\; \textrm{km}\cdot\textrm{h}^{-1}$ z Postoloprt po přímé silnici do Kožuchova v $8$ hodin ráno a za jeho uchem se v tu chvíli probouzí pilná včela Žofka. Současně z cílové vísky vzdálené $40\; \textrm{km}$ jim naproti startuje Žďorp a nasazuje tempo $25\; \textrm{km}\cdot\textrm{h}^{-1}$. Do okamžiku, než se oba potkají, musí Žofka, která je přeci jen dvakrát rychlejší než Mňága, plnit úkol spojovatelky – donese zprávu od M. k Ž., otočí se a letí zpět. Kolik kilometrů takto nalétá do okamžiku setkání, pokud
- je bezvětří
- vane vítr od Kožuchova (podél silnice) o rychlosti $10\; \textrm{km}\cdot\textrm{h}^{-1}$
- vane vítr kolmo na silnici o stejné rychlosti.
6. Série 7. Ročníku - S. trochu počítání
- Ze znalosti vztahů $\cosh^{2} a–\sinh^{2}a=1$ a tgh $a=\sinh a / \cosh a$ odvoďte vzorce použité v závěru výkladu mezi hyperbolickým cosinem resp. sinem a tangentou.
- Pokuste se v případě nějakého vhodného geometrického objektu dokázat, že se jeho plocha zachovává i po Lorentzovské transformaci souřadnic.
5. Série 2. Ročníku - S. Lorentzovy transformace
V posledním seriálovém příkladu se dotkneme transformací snad nejpopulárnějších – Lorentzových transformací. Na přelomu 19. a 20. století bylo přesnými pokusy změřeno, že světlo se pohybuje stejnou rychlostí vůči všem inerciálním soustavám. To zásadně odporuje běžné představě o prostoru a času – odporuje to prosté zkušenosti, že rychlosti se sčítají. Tento problém vyřešil r. 1905 A. Einstein ve svojí speciální teorii relativity. Tato teorie není založena na naší každodenní zkušenosti s malými rychlostmi, a proto se nesmíme zaleknout některých jejích zdánlivě zvláštních důsledků v oblastech, na které nejsme zvyklí. Změna představ na prostor a čas se hlavně odrazila v nahrazení Galileových transformačních vztahů mezi dvěma inerciálními soustavami pohybujícími se vzájemnou rychlostí $v$ ve směru osy $x$, které v čase nula splývají, $x′=x-vt$, $y′=y$, $z′=z$, $t′=t$, se vztahy Lorentzovými. Vaším úkolem bude nyní odvodit je. Využijeme k tomu zkušenosti z pomoci Severním království. Jak bylo v komentáři k seriálovému příkladu 3. série poznamenáno, transformační vztahy mezi $x$, $y$ a $x′$, $y′$ (viz komentář ke zmíněném příkladu) jsou jedinými, které zachovávají vzdálenost, tj. $Δx+(kΔy)=Δx′+(kΔy′)$. Využijeme něčeho podobného. Lze odvodit (provedeme v komentáři), že v našem případě dávají výrazy
$$Δx-(cΔt),Δx′+(cΔt′)\; (1)$$
stejné výsledky. Musíme tedy hledat takové transformace, které převádějí výrazy (1) jeden na druhý. Ve shodě s panem Einsteinem dále předpokládejme, že vztahy mezi souřadnicemi soustav $S$ a $S′$ ($S′$ se pohybuje rychlostí $v$ ve směru $x$ vůči $S$) jsou
$$x′=ax+bt,\; y′=y,\; z′=z,\; t′=cx+dt, \; a,\;b,\;c,\;d∈\textbf{R}\; (2)$$
a pro souřadnice počátku soustavy $S′$ platí $x_{p}/t_{p}=v,\; x_{p}′=0,\; y_{p}′=0,\; z_{p}′=0$. Najděte tedy transformace typu (2), které splňují (1). Uveďte postup!