Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (70)elektrický proud (75)gravitační pole (80)hydromechanika (146)jaderná fyzika (44)kmitání (56)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (295)mechanika plynů (87)mechanika tuhého tělesa (220)molekulová fyzika (71)geometrická optika (77)vlnová optika (65)ostatní (164)relativistická fyzika (37)statistická fyzika (21)termodynamika (153)vlnění (51)
matematika
5. Série 2. Ročníku - S. Lorentzovy transformace
V posledním seriálovém příkladu se dotkneme transformací snad nejpopulárnějších – Lorentzových transformací. Na přelomu 19. a 20. století bylo přesnými pokusy změřeno, že světlo se pohybuje stejnou rychlostí vůči všem inerciálním soustavám. To zásadně odporuje běžné představě o prostoru a času – odporuje to prosté zkušenosti, že rychlosti se sčítají. Tento problém vyřešil r. 1905 A. Einstein ve svojí speciální teorii relativity. Tato teorie není založena na naší každodenní zkušenosti s malými rychlostmi, a proto se nesmíme zaleknout některých jejích zdánlivě zvláštních důsledků v oblastech, na které nejsme zvyklí. Změna představ na prostor a čas se hlavně odrazila v nahrazení Galileových transformačních vztahů mezi dvěma inerciálními soustavami pohybujícími se vzájemnou rychlostí $v$ ve směru osy $x$, které v čase nula splývají, $x′=x-vt$, $y′=y$, $z′=z$, $t′=t$, se vztahy Lorentzovými. Vaším úkolem bude nyní odvodit je. Využijeme k tomu zkušenosti z pomoci Severním království. Jak bylo v komentáři k seriálovému příkladu 3. série poznamenáno, transformační vztahy mezi $x$, $y$ a $x′$, $y′$ (viz komentář ke zmíněném příkladu) jsou jedinými, které zachovávají vzdálenost, tj. $Δx+(kΔy)=Δx′+(kΔy′)$. Využijeme něčeho podobného. Lze odvodit (provedeme v komentáři), že v našem případě dávají výrazy
$$Δx-(cΔt),Δx′+(cΔt′)\; (1)$$
stejné výsledky. Musíme tedy hledat takové transformace, které převádějí výrazy (1) jeden na druhý. Ve shodě s panem Einsteinem dále předpokládejme, že vztahy mezi souřadnicemi soustav $S$ a $S′$ ($S′$ se pohybuje rychlostí $v$ ve směru $x$ vůči $S$) jsou
$$x′=ax+bt,\; y′=y,\; z′=z,\; t′=cx+dt, \; a,\;b,\;c,\;d∈\textbf{R}\; (2)$$
a pro souřadnice počátku soustavy $S′$ platí $x_{p}/t_{p}=v,\; x_{p}′=0,\; y_{p}′=0,\; z_{p}′=0$. Najděte tedy transformace typu (2), které splňují (1). Uveďte postup!
4. Série 2. Ročníku - 3. reflektor
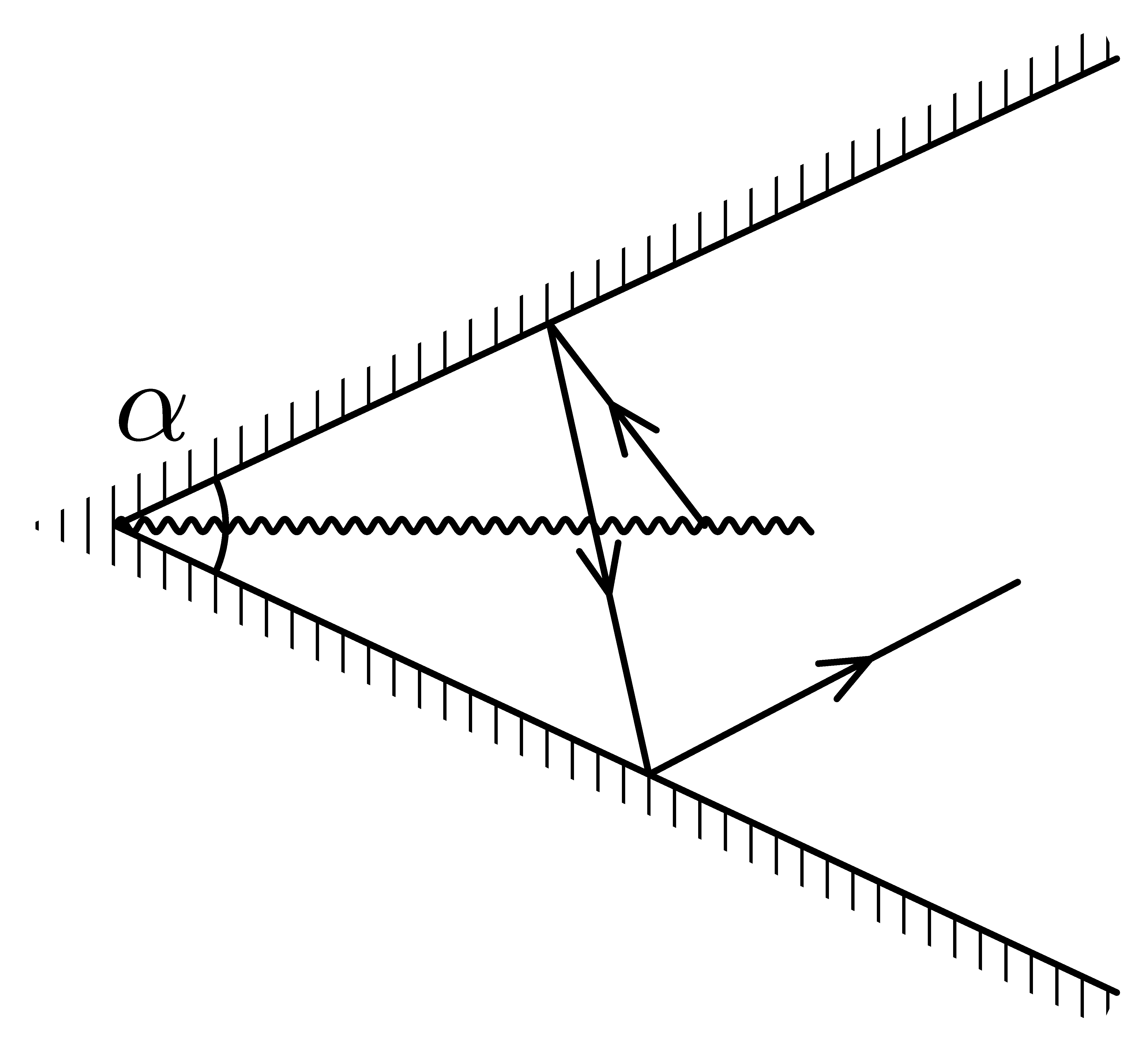
Reflektor
Jaký musí být vrcholový úhel kuželového reflektoru, aby se paprsky ze svítícího vlákna v ose kuželu délky $l$ odrazily o stínítko jednou, dvakrát, $n$-krát? Stínítko je dostatečně velké.
4. Série 2. Ročníku - S. polární souřadnice
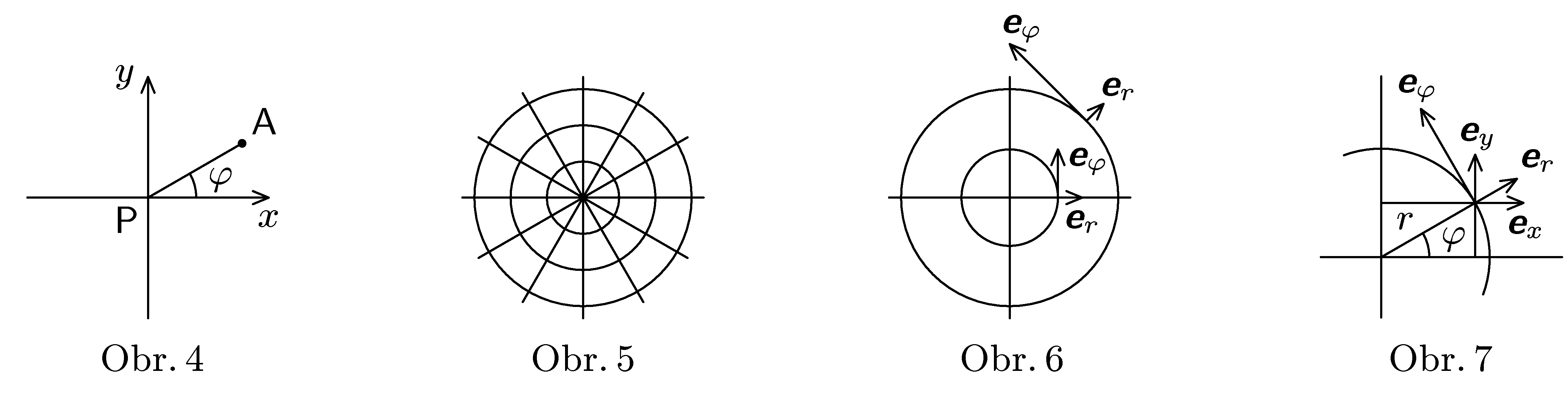
Polární souřadnice
- Polární souřadnice bodu A v rovině je dvojice čísel $r$, $φ$, udávající vzdálenost bodu $A$ od počátku a úhel polopřímky $PA$ a osy $x$ (obr. 4). Odvoďte transformační vztahy od polárních souřadnic $r$, $φ$ ke kartézským souřadnicím $x$, $y$.
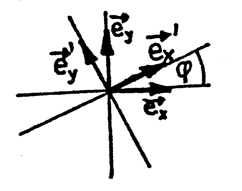
- U polárních souřadnic hraje roli souřadných os přímky procházející počátkem a kružnice se středem v počátku (obr. 5) - na těchto křivkách je vždy jedna souřadnice konstantní. Vektory báze se nyní volí v každém bodě tečné k souřadnicovým osám v tomto bodě a délky $|\textbf{e}_{r}|=1$, $|\textbf{e}_{φ}|=r$ (obr. 6). V tomto případě nejsou již vektory báze v různých bodech rovnoběžné, jak tomu bylo v případě kartézských souřadnic. Odvoďte transformační vztahy od souřadnic $b_{r}$, $b_{φ}$ k $b_{x}$, $b_{y}$ vektoru $\textbf{b}$ vedoucího z bodu $A$. Souřadnice $b_{r}$, $b_{φ}$ jsou počítané vůči bázi $\textbf{e}_{r}$, $\textbf{e}_{φ}$ v bodě $A$ (polární souřadnice), $b_{x}$, $b_{y}$ jsou počítané vůči bázi $\textbf{e}_{x}$, $\textbf{e}_{y}$ (kartézské souřadnice) a bod $A$ má polární souřadnice $r$, $φ$ (viz obr. 7).
3. Série 2. Ročníku - S. zeměměřiči podruhé
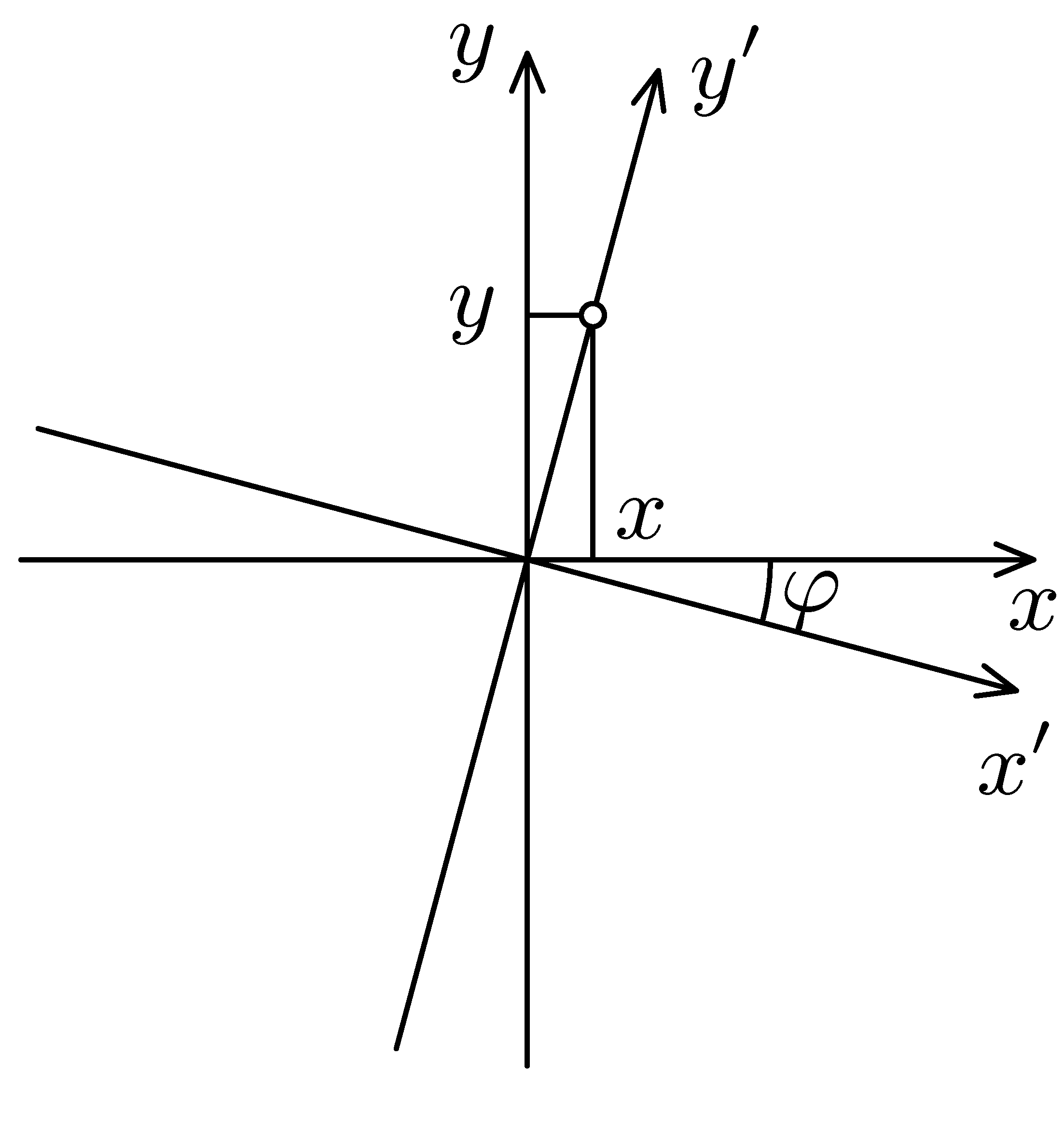
- Vraťme se opět do Severního království. V řešení příkladu I.S jste velkým zeměměřičům správně poradili převodní vzorce
$$x′=x\cos φ-yk\sin φ\; (1)$$ $$y′=kx\sin φ+y\cos φ\; (2)$$
kde $k$ je poměr metr ku severské míli a $φ$ úhel mezi magnetickým pólem a Severkou. Zeměřičům se však tento výsledek moc nelíbil, a to hned ze dvou důvodů – za prvé se v nich proti všem tradicím převádí severská míle na metr, s čímž se ale budou muset vyrovnat sami, ale hlavně za druhé neměří v Severním královstní odchylku mezi oběma používanými severními směry pomocí úhlu, ale pomocí tzv. odklonu $u$. Odklon osy $y′$ od osy $y$ je definován jako $u=x/y$, kde $x$ a $y$ jsou souřadnice bodu, který leží ve směru Severky, tj. osy $y$. Ukažte, že odklon $u$ nezávisí na tom, který bod na ose $y′$ v definici zvolíme, že odklon osy $y$ od $y′$ je $u$ a vyjádřete převodní vztahy (1) a (2) v závislosti na odklonu místo na úhlu.
- Zeměměřiči při porovnání svých výsledků zjistili zajímavou věc. Většina údajů se vlivem používání odlišných severních směrů liší, ale jeden údaj, který získávají podle vzorce $Δx+(kΔy)$, resp. $Δx′+(kΔy′)$, vychází oběma zeměměřičům stejně. Je to náhoda? Pokud ne, tak to dokažte a odůvodněte proč.
2. Série 2. Ročníku - S. vektory
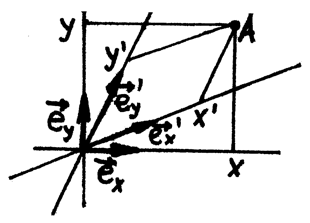
Dvě soustavy
Obecné soustavy
- Mějme zadané dvě soustavy souřadnic pomocí vektorů $\textbf{e}_{x}$, $\textbf{e}_{y}$ a $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ a společného počátku $P$. Vzájemnou polohu soustav máme zadanou pomocí souřadnic $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ vektorů $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ vůči bázi $\textbf{e}_{x}$, $\textbf{e}_{y}$. $\textbf{e}_{x}′=a_{xx} \textbf{e}_{x}+a_{xy} \textbf{e}_{y}$, $\textbf{e}_{y}′=a_{yx}\textbf{e}_{x}+a_{yy}\textbf{e}_{y}$. Odvoďte transformační vztahy mezi souřadnicemi $x$, $y$ a $x′$, $y′$ v závislosti na koeficientech $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ (tj. předpis, jak z $x$ a $y$ vypočítat $x′$ a $y′$ a naopak).
- Jelikož obě soustavy mohly být obecné (nepravoúhlé, bez stejných jednotek), bylo potřeba k zadání vzájemného vztahu soustav udat čtyři koeficienty $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$. Pokud budou obě soustavy kartézské (pravoúhlé s jednotkovým měřítkem), tak musí být délky vektorů $\textbf{e}_{x}$, $\textbf{e}_{y}$ resp. $\textbf{e}_{x}′$, $\textbf{e}_{y}′$ jednotkové a vektory musí být na sebe kolmé. K udání vzájemné polohy pak stačí zadat vzájemný úhel $φ$. Jak souvisí v tomto případě koeficienty $a_{xx}$, $a_{xy}$, $a_{yx}$, $a_{yy}$ s úhlem $φ$?
1. Série 2. Ročníku - E. sluneční čas
Jak víme, celý povrch Země je rozdělen na 24 hlavních časových pásem po 15 stupních zeměpisné délky. Na celém území naší republiky se řídíme středoevropským časem příslušejícím 15. stupni východní délky, resp. letním časem posunutým o 1 hodinu. Dále lze zavést tzv. sluneční čas, jehož poledne (12 hodin) je v okamžiku, kdy je na dané zeměpisné délce slunce nejvýše. Navrhněte metodu měření a změřte rozdíl mezi letním středoevropským časem a slunečním časem ve vaší zeměpisné délce. Výsledek porovnejte s výpočtem.
4. Série 1. Ročníku - 1. mouchy
Koule o poloměru $R$ pohybující se velkou rychlostí $v$ prolétne rojem much, který se pohybuje rychlostí $u$ kolmou na směr pohybu koule. Šířka roje je $d$, v jednotce objemu se nachází průměrně $n$ much. Kolik much přijde při této smutné události o život?
3. Série 1. Ročníku - S. jak se šíří drby?
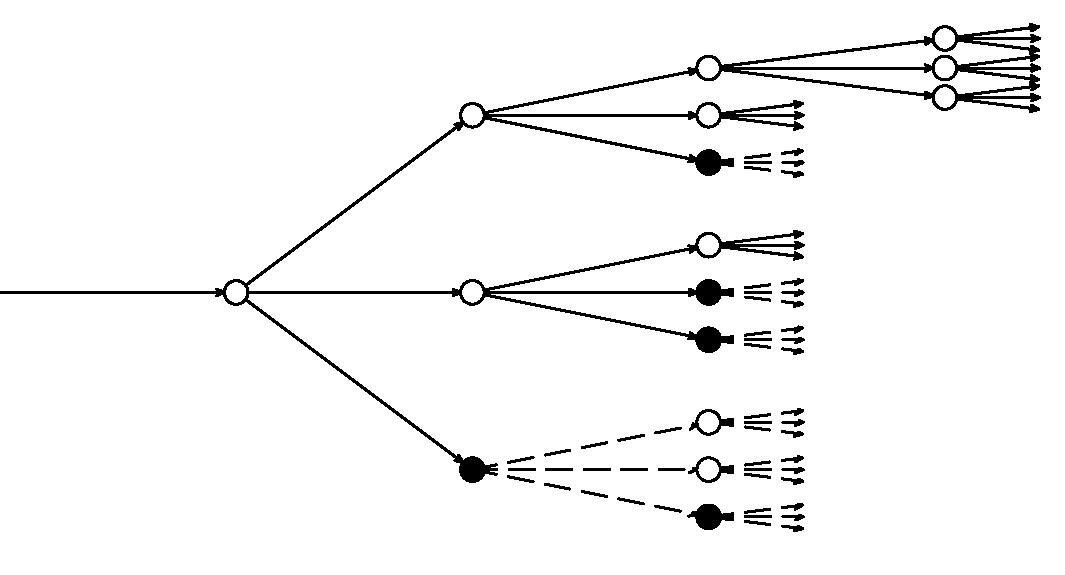
Schéma šíření drbů
Rozeberme model šíření drbů daný schematem na obrázku. Model je velice idealizovaný. Každý má šanci dozvědět se drb jen od jediného člověka, a je-li drbař, poví ho třem lidem. Ne každý člověk roznáší drby. Nedrbaře jsme na obrázku označili plným kolečkem a roznašeče drbů prázným. (Umístění nedrbařů je náhodné!) Koncentrace drbařů je $x$ (to znamená, že náhodně vybraný člověk ze sítě na obrázku je roznašečem drbů s pravděpodobností $x$.) Plné šipky na schematu označují cestu drbu, čárkované jen pokračování sítě, kde se drb již nešíří. Při $x$ blízkém 0 se drb poměrně brzy zastaví. Při $x$ blízkém 1 se bude šířit neomezeně.
Zjistěte (výpočtem, simulací na mikropočítači nebo třeba jen intuitivním argumentem) kriticku hodnotu $x_{c}$, při které se drb právě začne v průměru šířit neomezeně. Zkuste dále odhadnout, jaká část lidí se drb dozví při $x>x_{c}$. (Dovedete nalézt fyzikální proces, který by bylo možné alespoň přibližně takto modelovat?)
1. Série 1. Ročníku - 3. klavír
Předpokládejte, že vlastníte výborný koncertní klavír. Chcete ho nechat naladit. Pozvete nejlepšího ladiče pian. Ten ladí klavír tak, že porovnává zvuk klavíru a etalonu (ladičky). Jak dlouho mu bude trvat perfektní naladění klavíru?
- zhruba hodinu
- zhruba den
- zhruba týden
- zhruba měsíc
- nekonečně dlouho
1. Série 1. Ročníku - S. kapitán Brown
Představme si, že v přístavu vyšel z hospody H kapitán Brown. Kapitán je zcela opitý, a tak kráčí náhodně (krok vpřed i vzad jsou stejně pravděpodobné). Předpokládejme, že kráčí podél mola v přímkové dráze. Snaží se dojít ke své lodi, která kotví $k$ kroků od výchozího bodu H.
Nalezněte pravděpodobnost, že po $n$ krocích kapitán dojde ke své lodi. Úlohu se pokuste řešit analyticky, tj. přímo nalezněte hledanou pravděpodobnost $p=p(n,k)$. Úlohu se také pokuste modelovat. Pomocí vhodného generátoru náhodných čísel. (Zkuste třeba házet mincí, eventuelně použít mikropočítač atp.) nechte mnohokrát vyjít námořníka z počátečního bodu a sledujte v kolika pokusech dojde ke své lodi. (Zkuste číselně pro $n=20$, $k=8$).
Rozřešení předchozí úlohy použijte k zodpovězení této otázky: kapitán udělá $n$ kroků; jaká je střední hodnota druhé mocniny jeho vzdálenosti od bodu H?
Návod: Požadované střední hodnoty jsou definovány takto. $$\langle r\rangle=\sum_{k}p(n,k)\cdot k \langle r^2\rangle=\sum_{k}p(n,k)\cdot k^2$$ Potřebné pravděpodobnosti $p(n,k)$ můžete odhadnout z vašich modelových pokusů, i když je neznáte analyticky.
Dovedli byste zdůvodnit analogii mezi kráčením kapitána Browna s pohybem pylových zrnek v kapalině? Je z hlediska vámi spočtených středních hodnot $\langle r\rangle$, $\langle r^2\rangle$ podstatné, že kapitán Brown kráčí v přímce, kdežto pylová zrnka se pohybují v rovině?