Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (71)elektrický proud (75)gravitační pole (81)hydromechanika (146)jaderná fyzika (44)kmitání (57)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (298)mechanika plynů (87)mechanika tuhého tělesa (221)molekulová fyzika (71)geometrická optika (78)vlnová optika (65)ostatní (167)relativistická fyzika (37)statistická fyzika (21)termodynamika (154)vlnění (51)
elektrický proud
(4 body)2. Série 27. Ročníku - P. Temelínská
Odhadněte, kolik jaderného paliva se spotřebuje v jaderné elektrárně na $1\;\jd{MWh}$ elektrické energie, kterou spotřebují lidé až v domácnosti. Srovnejte to se spotřebou paliva v tepelné elektrárně. Nezapomeňte uvažovat všechny možné ztráty.
Bonus: Uvažte i energii, která se spotřebuje při těžbě a přepravě potřebných surovin.
Karel přemýšlel nad ČEZem.
(4 body)1. Série 26. Ročníku - 3. Poledniková
Nechť jsou podél poledníků a rovnoběžek natažené dráty, které jsou v místech křížení spojené. Jaký naměříme odpor mezi body sítě, které odpovídají zemským pólům, pokud víte, že odpor jednoho metru drátu je $ρ$. Poledníky i rovnoběžky uvažujte po 15$°$.
Bonus: Jaký je odpor mezi dvěma uzly sítě, které leží na rovníku a naproti sobě?
Honza Hum. honil Janapku po poledníku.
4. Série 23. Ročníku - P. úleva u ohradníku
Zamyslete se nad tím, jak je to s odporem tekoucího elektrolytu. Je jeho velikost závislá na tom, jestli teče po směru elektrického proudu v něm, nebo naopak? Zkuste odhadnout rozdíl, je-li.
ránu dostal Grepe
6. Série 22. Ročníku - 1. odpor je marný
Vypočítejte odpor $n$-rozměrné krychle mezi dvěma nejvzdálenějšími vrcholy (ty o souřadnicích $(0$, $0$, …, $0)$ a $(1$, $1$, …, $1)$. Zkuste začít od trojrozměrné a použijte stejný postup.
Přednesl Lukáš Ledvina
4. Série 22. Ročníku - P. zachraňte fyziku
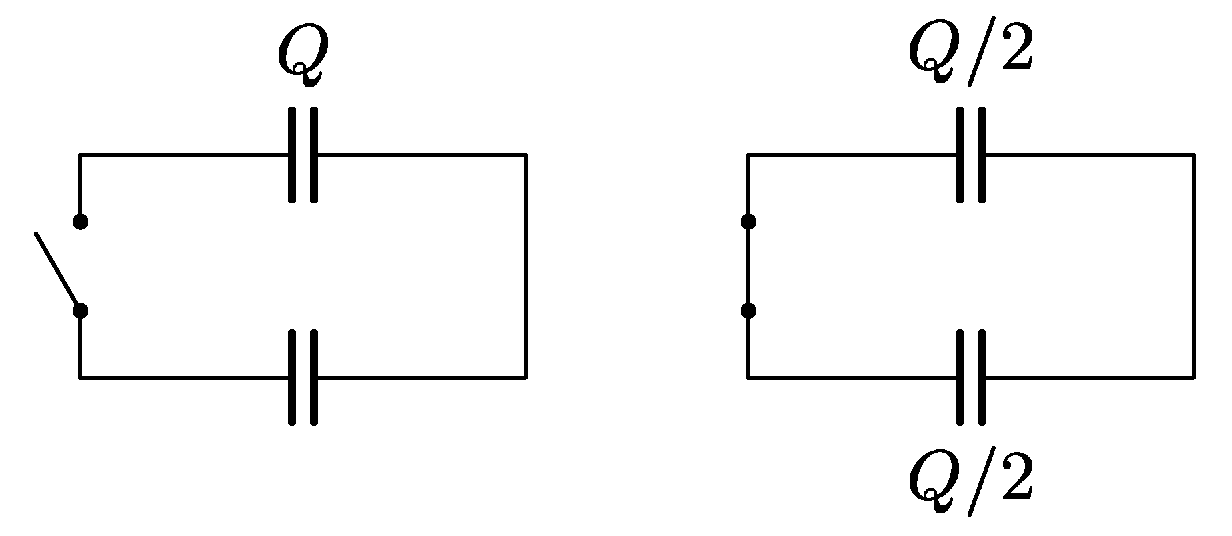
Rozpojený obvod na obrázku obsahuje jeden nenabitý a jeden nabitý kondenzátor (náboj $Q)$. Vodiče jsou ideální, nemají žádný odpor, oba kondenzátory jsou stejné. Celková energie nábojů v obvodu tedy je $Q⁄2C$. Pokud se po sepnutí vypínače náboje na kondenzátorech vyrovnají, celková energie bude $Q⁄8C+Q⁄8C=Q⁄4C$, což je polovina oproti počáteční situaci. Vysvětlete tento rozdíl. Kde se spotřebovala polovina energie? Vypínač je vyrobený tak šikovně, že v něm vysvětlení netkví.
S touhle záludností přišel Jarda Trnka.
3. Série 21. Ročníku - S. bloudění námořníka, pí-obvod a epidemie v Praze
Integrál
Integrujte metodou Monte Carlo funkci $e^{-x^2}$ na intervalu $[ -100,100]$. Zkuste také numericky určit hodnotu tohoto integrálu od $-∞$ do $+∞$.
Návod: Funkce je symetrická vůči počátku, čili ji stačí integrovat na intervalu $[ 0, +∞ )$. Proveďte substituci $x=1⁄t-1$, čímž změníte meze integrálu od $0$ do $1$.
Bloudění námořníka
Opilý námořník vstoupil na molo dlouhé 50 kroků a široké 20 kroků. Jde směrem k pevnině. Při každém kroku dopředu však zavrávorá zároveň o krok nalevo nebo napravo. Zjistěte, s jakou pravděpodobností námořník dojde až na břeh a s jakou pravděpodobností spadne do moře a utopí se.
Námořník měl štěstí a neutopil se. Druhou noc se však opět vydává opilý z lodi na pevninu. Tentokrát však vane stálý vítr o rychlosti $3 \,\jd{m. s^{-1}}$, který způsobí to, že na jednu stranu udělá krok s pravděpodobností 0,8 a na druhou stranu s pravděpodobností 0,2. Zjistěte, s jakou pravděpodobností námořník dojde až na břeh a s jakou pravděpodobností spadne do moře a utopí se.
Třetí noc se námořník opět vydává opilý na pevninu. Tentokrát však vane proměnlivý vítr. Vane podle normálního rozdělení se střední hodnotou $0\,\jd{ m.s^{-1}}$ a disperzí $2\,\jd{ m. s^{-1}}$. Zjistěte, s jakou pravděpodobností tentokrát námořník dojde až na břeh a s jakou pravděpodobností spadne do moře a utopí se. Můžete uvažovat, že námořník jde pomalu a setrvačnost větru lze zanedbat. Komu by to vadilo, nechť vymyslí, jak by vítr v po sobě jdoucích krocích koreloval.
Pí-obvod
Máme k dispozici 50 rezistorů o odporech $50\,\jd{ Ω}$ a chceme z nich sestavit obvod, jehož celkový odpor v ohmech bude co nejblíže číslu $π$. Pokuste se metodou simulovaného žíhání najít obvod, který by tomuto požadavku vyhovoval co nejlépe.
Pro určování celkového odporu obvodu si můžete přizpůsobit program, který najdete na našich webových stránkách.
Pokud se na tento úkol necítíte, můžete zkusit zahrnout do problému obchodního cestujícího zakřivení zemského povrchu a pokusit se jej vyřešit pro nějakou konkrétní množinu měst na Zemi (například všechna hlavní města v Evropě, USA atd.).
Epidemie v Praze
Zkoumejte vývoj epidemie v Praze, uvažujte 1 milión obyvatel. Intenzita nákazy $β$ je $0,4⁄1000000$ za den, uzdravení $γ$ je ( čtyřidny )^{$-1$}. Na počátku je nakaženo 100 lidí. Porovnejte průběh epidemie při očkování předem dvaceti procent lidí s průběhem epidemie při očkování až během epidemie s rychlostí půl procenta denně. A také s průběhem bez očkování. Konec epidemie vyhlásíme, bude-li méně jak 20 lidí nemocných.
Je spousta údajů, které můžete z počítačové simulace získat. Krom středovaného průběhu epidemie uveďte pro zajímavost též graf, kde ukážete prvních pět náhodných simulací. Dále můžete sledovat fluktuace. Můžete též výsledky porovnat s deterministickým modelem, když neuvažujete náhodnost nakažení. Těžištěm hodnocení bude, kolik různých zajímavých dat dokážete hezky zpracovat.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.
6. Série 20. Ročníku - 3. čtverák čtverec
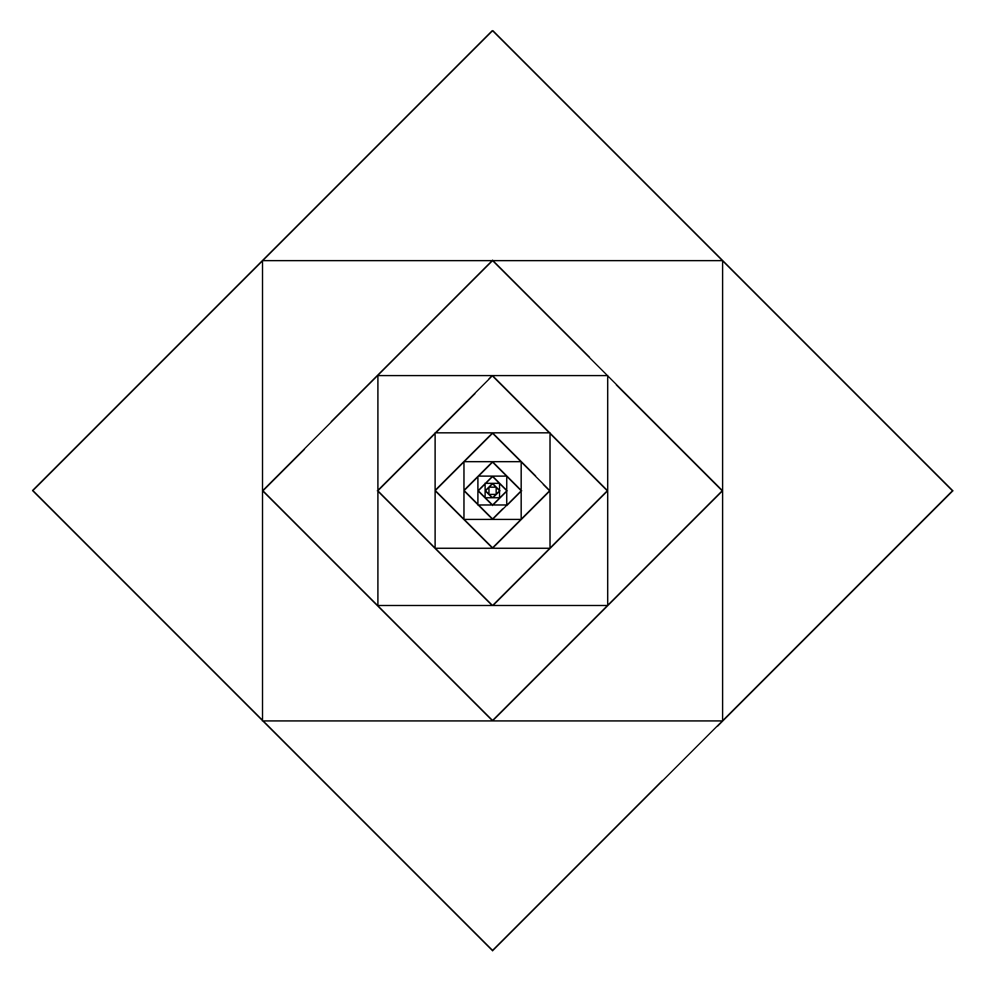
Obvod na obrázku vznikne spojením nekonečně mnoha drátěných čtverců, přičemž každý následující je √2 -krát menší. Drát, ze kterého je obvod vyroben, o délce rovné straně největšího čtverce má odpor $R$. Určete odpor obvodu mezi krajními body vlevo a vpravo.
Úlohu vymyslel Marek Pechal.
2. Série 18. Ročníku - 2. kolik drátů na sloupech?
Kolikafázové napětí bychom museli používat, aby efektivní hodnota napětí fáze-zem byla stejná jako efektivní hodnota napětí mezi dvěma sousedními fázemi?
Úlohu navrhl Pavel Augustinský.
2. Série 18. Ročníku - 4. zoufalí trosečníci
Trosečníci na severním pólu si chtějí zpříjemnit chvíli před blížící se smrtí posledním šálkem kávy. Poraďte jim, jak si mají ohřát vodu, aby se jí dostalo na co nejvíce z nich. Se svými skromnými technickými prostředky mohou ohřev realizovat následujícími způsoby:
- Akumulátor o vnitřním odporu $2R$ přímo připojí k topné spirále o odporu $R$.
- Tentýž akumulátor připojí do série s topnou spirálou a kondenzátorem. Pokaždé, když se kondenzátor nabije, jej z obvodu vytáhnou a připojí obráceně.
- Tímtéž akumulátorem budou střídavě nabíjet kondenzátor a vybíjet ho přes topnou spirálu.
Vymyslel Matouš Ringel, když si na výletě vařil kávu.
3. Série 17. Ročníku - 3. odporová síť
Jaký je odpor mezi body $A$ a $B$ odporové sítě na obrázku? Svislé úsečky mají odpor $R$ a vodorovné odpor nemají. Síť je nekonečná, na obrázku je z technických důvodů jen konečná iterace.
Vynalezl Pavel Augustinský pro Bělčickou olympiádu.