Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (70)elektrický proud (75)gravitační pole (80)hydromechanika (146)jaderná fyzika (44)kmitání (56)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (295)mechanika plynů (87)mechanika tuhého tělesa (220)molekulová fyzika (71)geometrická optika (77)vlnová optika (65)ostatní (165)relativistická fyzika (37)statistická fyzika (21)termodynamika (153)vlnění (51)
astrofyzika
5. Série 24. Ročníku - 2. Měsíc jako lodička
Z jakých míst na Zemi a kdy vypadá Měsíc jako lodička? (jeho cípy jsou rovnoběžné s obzorem, osa symetrie je kolmá k místnímu nebeskému poledníku) Pokud si s řešením nevíte rady, můžete si nainstalovat vhodný software (např. Celestia) a celou situaci si prohlédnout z různých míst na zemi.
Terka J. se jednou ve čtyři ráno zasněně dívala na Měsíc
1. Série 24. Ročníku - 1. rozcvička
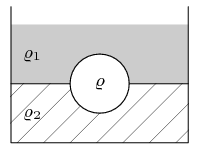
- mezi vodami
Na rozhraní dvou nemísitelných kapalin se vznáší pevná homogenní koule o hustotě ρ (viz obrázek). Horní kapalina má hustotu $ρ_{1}$, dolní $ρ_{2}$, přičemž víte, že $ρ_{1} < ρ < ρ_{2}$. Jaká část objemu koule se nachází v horní a jaká v dolní kapalině?
- sesterská planeta
V posledních několika letech již byla objevena spousta planet ležících mimo Sluneční soustavu. Daleko zajímavější by bylo ovšem objevovat planety, které jsou podobné Zemi. Předpokládejte, že chcete objevit podobnou Zemi (terestrická planeta s podobným poloměrem jako Země), která obíhá svou hvězdu podobnou Slunci (stejná spektrální třída – podobná hmotnost, podobný poloměr) jednou za pozemský rok. Předpokládejte, že tato soustava je vzdálená od našeho Slunce zhruba 10 pc. Určete podmínky, za kterých by šlo pozorovat planetu přímo z poklesu jasnosti hvězdy a odhadněte dobu, na kterou tato situace nastane. Jak se zkomplikuje hledání takové hvězdy, když soustava bude mít víc planet?
Z ruských bylin vyčetl Marek a po hvězdných dálavách zatoužil Karel.
1. Série 22. Ročníku - P. Mikuláš vs. Klaudios
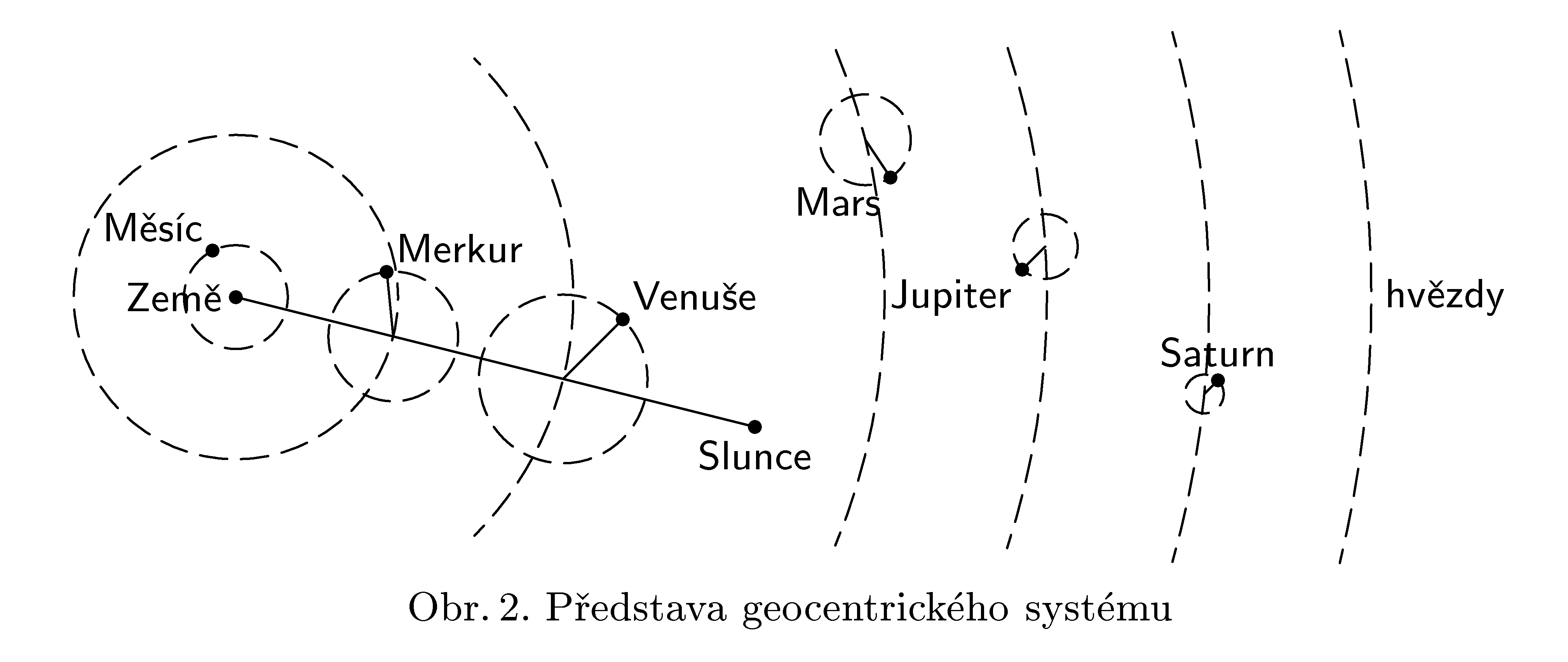
Představa geocentrického systému
Rok 2009 je vyhlášen jako Mezinárodní rok astronomie a připomíná 400 let používání dalekohledů lidstvem. Vraťme se o čtyři staletí zpět, kdy byl dalekohled již k dispozici, ale klasická fyzika ještě v plenkách. V otázce uspořádání světa spolu soupeřily Koperníkův heliocentrický názor a Ptolemaiův geocentrický systém. Navrhněte experiment, resp. pozorování, které mezi oběma představami dokáže rozhodnout. Dostatečně okomentujte, jaký výsledek lze očekávat a co z něj plyne v prospěch či neprospěch uvažovaných uspořádání. Vlastní pozorování není nutné, i když vhodné. Navíc vysvětlete, proč jsou v geocentrickém modelu Slunce a Země spojeny úsečkou?
Významný důkaz chtěl připomenout Pavel Brom.
5. Série 21. Ročníku - 4. sluneční konzerva
Ráma cestuje mezi hvězdami tak, že polovinu času rovnoměrně zrychluje a polovinu času rovnoměrně zpomaluje. Právě se pohybuje kolem Slunce po parabole s vrcholem na orbitě Země. Energii získává ze slunečního záření (žádný reaktor nebo obří baterie jsi na něm neobjevil) a jeho povrch absorbuje 80 % dopadající energie. Nasbírá při průletu sluneční soustavou dostatečnou energii, aby se dostal k Siriu, který je vzdálen 12 světelných let, za 24 let?
Nadhodil Jakub Benda
5. Série 21. Ročníku - S. posloupnosti, horká dutina a bílý trpaslík
- Odvoďte Taylorův rozvoj exponenciály a pro $x=1$ graficky znázorněte posloupnost částečných součtů řady $\sum_{k=1}^{∞}1⁄k!$ spolu s posloupností ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$.
Stejným způsobem porovnejte posloupnost ${ ( 1 - 1 ⁄ n)^{n}}_{n=1,2,\ldots}$ a posloupnost částečných součtů řady $\sum_{k=1}^{∞}x^{k}⁄k!$, čili posloupnost ${\sum_{k=1}^{n}x^{k}⁄k!}_{n=1,2,\ldots}$, tentokráte však pro $x=-1$.
- Druhý úkol bude určit závislost koncentrace elektronů a pozitronů na teplotě při celkovém náboji $Q=0$ v prázdné uzavřené horké dutině.
(Bude-li se vám chtít, i při jiných vámi zvolených hodnotách $Q.)$ Dále určete závislost poměru vnitřní energie $U_{e}$ elektronů a pozitronů ku celkové vnitřní energii systému $U$ (tj. součtu energie elektromagnetického záření a částic) na teplotě a určit hodnoty teploty odpovídající některým význačným hodnotám tohoto poměru (např. 3 ⁄ 4, 1 ⁄ 2, 1 ⁄ 4, …; může tento poměr nabývat všech těchto hodnot?).
Pokuste se své výsledky pěkně graficky zpracovat ve formě grafů (můžete zkusit i trojrozměrné).
Při vašem snažení vám může hodně pomoci, pokud si zavedete vhodné bezrozměrné jednotky (např. $βE_{0}$ místo $β$ apod.).
- Řešte soustavu diferenciálních rovnic pro $M(r)$ a $ρ(r)$ v modelu bílého trpaslíka pro několik vhodně zvolených hodnot $ρ(0)$
a pro každou z nich sledujte hodnotu, ke které se blíží $M(r)$ při $r→∞$. Ta je zřejmě rovna hmotnosti celé hvězdy. Pokuste se prozkoumat závislost této celkové hmotnosti na $ρ(0)$ a odhadnout její horní mez. Srovnejte váš výsledek s horní mezí hmotnosti bílého trpaslíka, kterou najdete v literatuře nebo na internetu. Uvažujte, že je hvězda tvořena héliem.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.
3. Série 21. Ročníku - 2. výtah až do nebe
Určete, jaké fyzikální vlastnosti musí mít materiál závěsného lana výtahu, který spojuje povrch Země a oběžnou geostacionární dráhu. Je vůbec takový materiál na Zemi dostupný?
Zadal Aleč Podolník.
3. Série 21. Ročníku - E. zkoumáme pohyb Slunce
Změřte co nejpřesněji výšku Slunce nad obzorem v pravé poledne a dobu od východu středu slunečního disku do jeho západu. Odvážlivci se mohou pokusit vypočítat teoretickou délku dne a hodnoty srovnat a okomentovat případný nesoulad.
Experimentální úlohu navrhl Pavel Brom.
1. Série 21. Ročníku - 3. vážíme si Slunce
Navrhněte několik metod ke stanovení (odhadu) hmotnosti Slunce, dostatečně je vysvětlete a vypočtěte podle nich hmotnost naší nejbližší hvězdy.
K zahřátí mozků do nového ročníku FYKOSu zadal Pavel Brom.
6. Série 20. Ročníku - 4. zákrytová dvojhvězda
Magnituda jisté zákrytové dvojhvězdy se mění se čtyřdenní periodou v této posloupnosti:
vedlejší minimum $m = 3,5$ ,
maximum $m = 3,3$ ,
hlavní minimum $m = 4,2$ ,
maximum $m = 3,3$ .
Větší složka této dvojhvězdy má také vyšší teplotu než její průvodce. Za předpokladu, že Země leží v oběžné rovině dvojhvězdy, vypočítejte magnitudy jednotlivých složek a poměr jejich délkových rozměrů. Převodní vztah mezi magnitudou $m$ hvězdy a osvětlením $E$, které způsobuje, je
$m=-2,5\log(E⁄E_{0})$,
kde $E_{0}$ je pevně definovaná hodnota.
Nepoužitá úloha z archivu.
3. Série 20. Ročníku - 3. vzdálenost vizuální dvojhvězdy
Z redukovaných hvězdných spekter složek dvojhvězdy (podle přítomných spektrálních čar, z nichž žádná v tomto případě nemění svou polohu v čase) jsme určili spektrální třídy obou hvězd a následně odhadli jejich hmotnosti na 2 a 3 hmotnosti Slunce. Z pozorování dalekohledem s ohniskovou vzdáleností 3 m víme, že složky skutečně obíhají v neměnné vzdálenosti 5 úhlových minut od sebe jednou za 50 let.
Dokážete z těchto informací určit vzdálenost dvojhvězdy od Slunce? Pokud ano, uveďte, jak jste jednotlivé informace použili, anebo nepoužili, a výsledek vhodně zaokrouhlete. Také okomentujte, jaký vliv na něj má nepřesná znalost údajů, zejména hmotností.
Při astronomickém pozorování vymyslel Pavel Brom.