Vyhledávání úloh podle oboru
Databáze úloh FYKOSu odjakživa
astrofyzika (85)biofyzika (18)chemie (23)elektrické pole (70)elektrický proud (75)gravitační pole (80)hydromechanika (146)jaderná fyzika (44)kmitání (56)kvantová fyzika (31)magnetické pole (43)matematika (89)mechanika hmotného bodu (295)mechanika plynů (87)mechanika tuhého tělesa (220)molekulová fyzika (71)geometrická optika (77)vlnová optika (65)ostatní (164)relativistická fyzika (37)statistická fyzika (21)termodynamika (153)vlnění (51)
molekulová fyzika
5. Série 14. Ročníku - 2. dělo na lodi
Děla na bitevních lodích se nabíjejí následujícím způsobem: do hlavně se dá střela o hmotnosti $M$ a za ní určitý počet balíku s výbušninou (objem jednoho balíku je $V_{0})$, podle toho jak daleko chceme střílet. Kolikrát se zvětší dostřel takového děla, když nabijeme dvojnásobné množství výbušniny? Výbuch si představujte tak, že najednou se místo výbušniny objeví dvouatomový plyn o teplotě $T_{0}$ a tlaku $p_{0}$. Ráže děla je deset palců. Odpor vzduchu zanedbejte.
Nápad Karla Kouřila, když přemýšlel, co zadáme do FYKOSu.
4. Série 14. Ročníku - 1. vesmírná stříkačka
Představte si, že ve vakuu mimo gravitační pole stříkáme vodní paprsek. Kromě tohoto paprsku je zde kolmo (mimoběžně) k jeho původnímu směru umístěn nabitý nekonečný drát s délkovou hustotou náboje $\lambda$. Voda je stříkána z velmi velké vzdálenosti s počáteční rychlostí $v$. Vzdálenost přímky, ve které je stříkána voda (ve které se na začátku pohybuje vodní paprsek) a drátu je $d$. Spočtěte úhel, o který se odchýlí vodní paprsek od původního směru. Molekuly vody si představte jako elektrické dipóly, jejich vzájemné působení zanedbejte a také zanedbejte jejich moment setrvačnosti (tj. představte si, že všechna hmotnost molekuly je soustředěna uprostřed mezi náboji, které jsou nehmotné).
Zadal Karel Kouřil unešen odchylováním vody tekoucí z kohoutku pomocí nabitého hřebínku.
3. Série 14. Ročníku - 3. dnem vzhůru
Ve velké nádobě s vodou je částečně ponořena dnem vzhůru válcová sklenice. Hladina vody v nádobě i ve sklenici je stejná a je vzdálena $l=10\jd{ cm}$ ode dna sklenice. Teplota vzduchu je $t_{0}=20\jd{^{\circ}C}$ a atmosférický tlak je $p_{0}=100\jd{ kPa}$. O jakou výšku $h$ stoupne hladina vody ve sklenici, jestliže se teplota sníží o $\Delta t=10\jd{^{\circ}C}$ a tlak stoupne o $\Delta p=2,0\jd{ kPa}$?
Počítalo se na cvičení k přednášce Fyzika I, zadal Honza Houštěk.
3. Série 14. Ročníku - 4. výpar vody
Za jak dlouho se vypaří voda ze sklenice o výšce $h=10\,\jd{cm}$ za normálních podmínek? Předpokládejte, že vlhkost vzduchu těsně nad hladinou je neustále $99\%$
Úlohu navrhl Karel Kouřil.
2. Série 14. Ročníku - P. problémovka z vody
O prázdninách byli někteří organizatoři FYKOSu sjíždět Vltavu a při této příležitosti je napadlo několik problémků, se kterými by od vás potřebovali poradit.
- Za jak dlouho doteče voda z Českého Krumlova do Prahy?
- Na jakou stranu alumatky (hliníkové karimatky, která má z jedné strany hliníkovou fólii a z druhé izolační pěnu) je výhodné si lehnout?
- Jak se v makarónech dělají díry?
Autor Lenka Zdeborová, inspirace: jak jinak než prázdninová Vltava.
1. Série 14. Ročníku - E. natahování špaget
Určete Youngův modul pružnosti v tahu uvařených špaget.
Bláznivý nápad Honzy Houšťka.
5. Série 12. Ročníku - 1. jehla na vodě
Určete maximální průměr ocelové jehly, která se ještě udrží na vodní hladině. Jehla je pokryta tenkým olejovým filmem, aby ji voda nesmáčela. Znáte hustotu oceli, vody a povrchové napětí vody. Pokud řešení problému závisí na délce jehly, pokládejte ji za známou a diskutujte její vliv.
1. Série 11. Ročníku - E. meření difúze ve sklenici vody
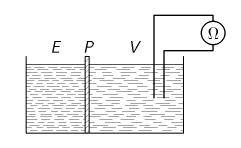
Námětem první experimentální úlohy je jev difúze v kapalině. V kádince je přepážkou $P$ oddělena voda $V$ od roztoku elektrolytu $E$ (např. roztok kuchyňské či jiné soli), viz obrázek. V čase $t_{0}=0 \,\jd{s}$ přepážku odstraníte a ohmmetrem budete sledovat pokles elektrického odporu s časem. Po měření vysvětlete kvalitativně a kvantitativně pozorované změny.
1. Série 11. Ročníku - P. je narušen druhý termodynamický princip?
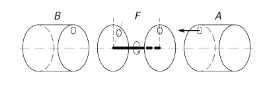
Mějme aparaturu, jejíž schéma je na obrázku. Molekuly opouštějící nádobu s plynem $A$ (teplota $T_{A}$, střední kvadratická rychlost molekul $v_{A})$ tvoří molekulární svazek, jež dále prochází rychlostním filtrem $F$. Pouze částice s rychlostí $v_{F}$ proletí až do nádoby $B$. V prostoru mezi deskami filtru je vakuum, střední volná dráha molekul je větší než rozměr aparatury. Při vhodné volbě rychlosti $v_{F}$ ($v_{F}$ > $v_{A})$ bude teplota nádoby $B$ vyšší než nádoby $A$. Tudíž teplo z tělesa chladnějšího ($A)$ bude přecházet na těleso teplejší ($B)$, což je ve sporu s druhým principem termodynamiky. Vaším úkolem je vysvětlit (ne)správnost této úvahy.
6. Série 10. Ročníku - 1. kapalina mezi rovnoběžnými deskami
Odvoďte vztah pro výšku $h$ hladiny kapaliny mezi dvěma svislými nekonečně dlouhými rovinami, vzdálenými od sebe $d$, které jsou ponořeny do kapaliny. Povrchové napětí kapaliny je $σ$ a hustota je $ρ$.