Vyhledávání úloh podle oboru

Když si vezmete běžné plastové brčko (slámku) a otřete ho kapesníkem, dokážete brčko nabít tak, že bude dokonce držet na některých stěnách a nástěnkách díky svému náboji. Vysvětlete jev a odhadněte, jak velký náboj dokážete na brčku vytvořit.

Nápověda: Hodilo by se použít dvě brčka.

• Spočtěte specifický odpor vodíkového plazmatu při teplotě 1 keV a srovnejte ho s odporem běžně používaných vodičů.

• Spočtěte, jak velký proud plazmatu je zapotřebí k vytvoření dostatečně silného poloidálního magnetického pole v tokamaku, který má hlavní poloměr 0,5 m. Toroidální pole vytváří cívky navinuté okolo torusu s hustotou vinutí 20 závitů na metr, kterými prochází proud 40 kA. Poloidální pole by mělo mít velikost zhruba 1 ⁄ 10 pole toroidálního.

• Pokuste se libovolným nápaditým způsobem vytvořit fyzický model siločar v tokamaku, tento model nafoťte a pošlete spolu s řešením.

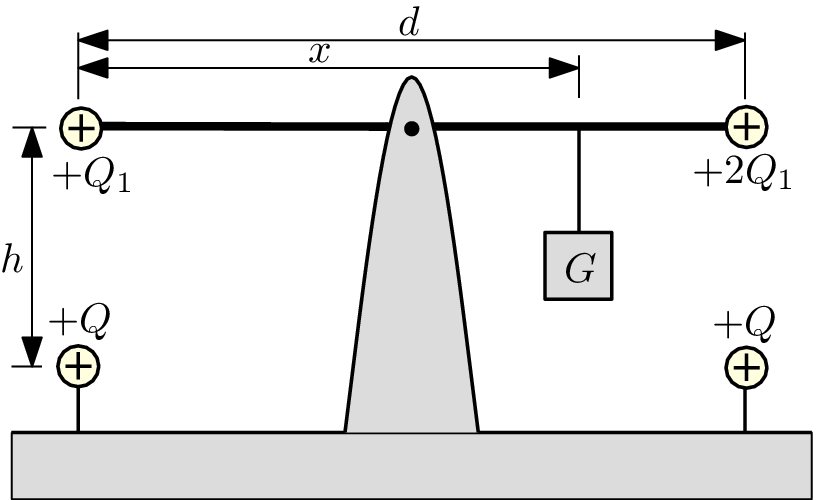
Na obrázku je nevodivá tyč délky $d$ zanedbatelné hmotnosti, otočná kolem svého středu. Na obou koncích tyče jsou připevněny malé vodivé koule zanedbatelných hmotností s kladnými náboji $Q_{1}$ a 2$Q_{1}$. Tyč je vyvážena závažím o tíze $G$ podle obrázku. Ve vzdálenosti $h$ přímo pod každou z koulí je pevně umístěna koule s kladným nábojem $Q$.

• Určete vzdálenost $x$, pro niž je tyč vodorovná a je v rovnováze.
• Pro jakou hodnotu $h$ bude tyč v rovnováze a nebude přitom vůbec zatěžovat čep, na němž je upevněna?

Mějme dvě nekonečně velké vodivé roviny, které jsou obě uzemněné a vzdálené od sebe $l$. Mezi nimi je umístěn bodový náboj velikosti $q$ ve vzdálenosti $x$ od horní roviny. Určete náboj indukovaný na spodní rovině.

Mezi dvěma opačně nabitými deskami se sem a tam odráží vodivá kulička zanedbatelných rozměrů. S jakou frekvencí se pohybuje? Napětí mezi deskami je $U$. Při nárazu se kulička nabije na náboj velikosti $Q$ shodný s polaritou desky. Koeficient restituce je $k$.

Bonus: Odpovídá výkon na tomto rezistoru energetickým ztrátám při nárazech?

Poznámka: Koeficient restituce je poměr kinetických energií po nárazu a před ním.

Jak všichni víme, kladné a záporné elektrické náboje jsou ve vesmíru v rovnováze, jinak by elektrická odpudivá síla překonala gravitační a tělesa by nedržela pohromadě. Ale je ta rovnováha dokonalá? Co když jsou všechna tělesa ve vesmíru nepatrně kladně (nebo záporně) nabita a odpudivá elektrická síla snižuje účinek gravitace. Jak by se taková nerovnováha projevila? Navrhněte způsob, jak tuto nerovnováhu zjistit a odhadněte, jakou nejmenší nerovnováhu jsme touto metodou schopni určit. Nerovnováhou myslíme celkový/(kladný-záporný) náboj v nějakém velkém objemu.

• Dopočtěte fyzikální význam konstanty $a$ pro funkci $f(z)=a\rm{i}⁄z$, znáte-li délkovou hustotu náboje $τ$.

• Vypočítejte a nakreslete ekvipotenciály a silokřivky pole v okolí rohu,

který má vrcholový úhel $θ$.

Nápověda: použijte funkci tvaru $w(z)=Az^{s}$, kde $s$ je vhodná reálná konstanta.

• Určete pole, které generuje elektrický dublet. Dublet jsou dvě tyče vzdálené $d$ s opačnou nábojovou hustotou, přičemž

$dτ=\;\mathrm{konst}$. Zajímá nás limita $d→0$.

Nápověda: platí ln$(1+x)≈x$ pro $x$ blízké 0.

• Rozmyslete si, co se stane, pokud existující komplexní potenciál $w(z)$

zobrazíme jinou holomorfní funkcí $v(z)$. Bude potenciál tvaru $v(w(z))$ i nadále řešit rovnice elektrostatiky?

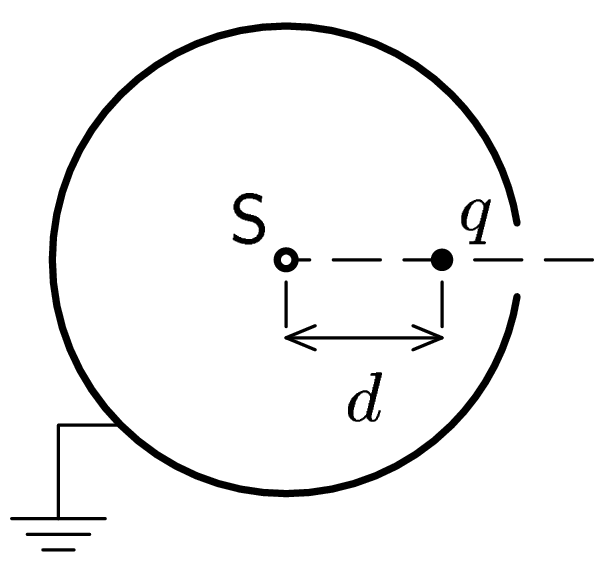
V uzemněné kouli z vodivého materiálu je vyvrtán malý otvor, tak akorát, že ním projde malá nabitá částice. Umístíme ji do vzdálenosti $d$ od středu koule na spojnici jejího středu a otvoru (viz obrázek). Náboj pustíme. Jak daleko z koule vyletí ven? Zkuste využít metodu zrcadlového potenciálu.

1. Druhým způsobem, kterým měřil J. J. Thomson velikost měrného náboje elektronu, je právě studium vychylování katodového záření elektrickým polem. Uvažujte aparaturu podle obrázku. Jak závisí odchylka paprsku, zaznamenaná na stínítku vpravo, na přiloženém napětí, rychlosti „corpuscules“ a geometrických vlastnostech aparatury?
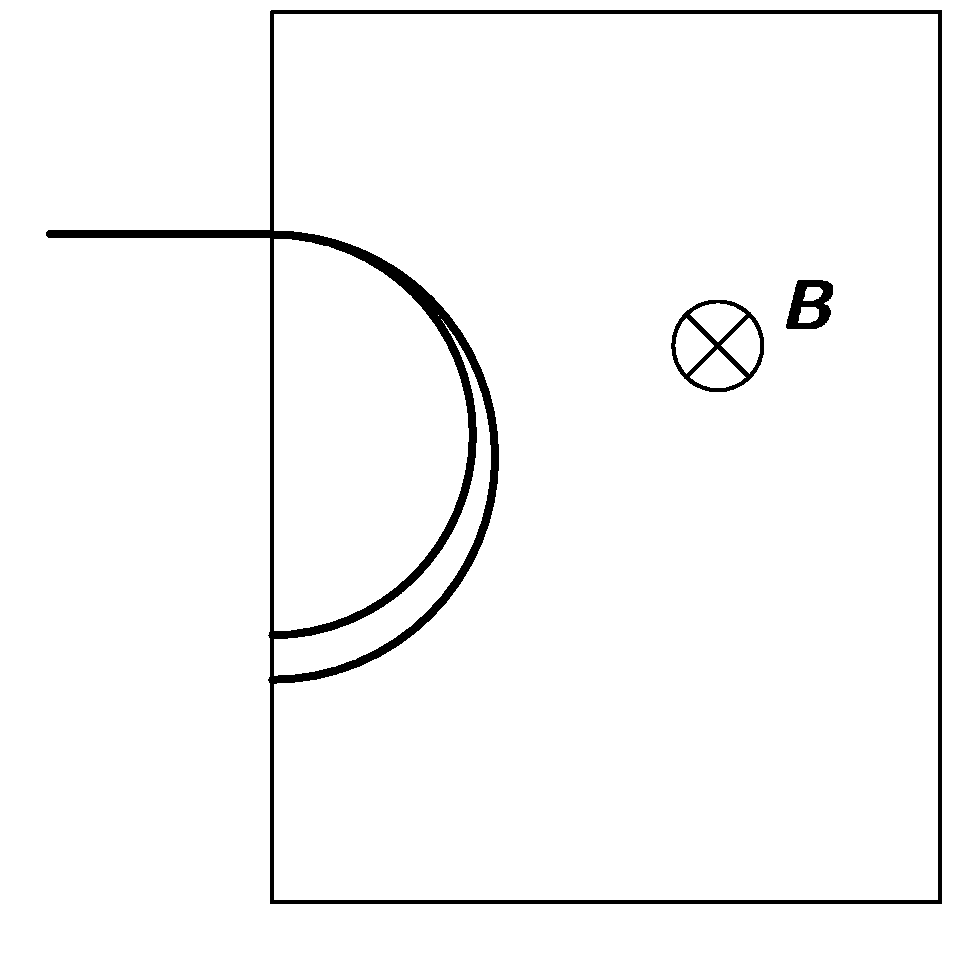
2. Jedním z problémů, se kterými se J. J. Thomson potýkal při stanovování měrného náboje elektronů, byl následující: Po vstupu paprsku katodového záření do magnetického pole se paprsek rozšířil do tvaru jakéhosi vějíře (viz obrázek). Tento rozptyl paprsku činí určování poloměru kružnice, kterou katodové záření vytvoří, značně nepřesné (Thomson hovořil o 20 %). Čím můžeme tento rozptyl vysvětlit? Pokud uvedete, jakým způsobem by bylo možno tuto nepřesnost zmenšit, vysloužíte si bonusový bod.
3. Zpracováním dat z tabulky určete velikost náboje elektronu v případě, že by olej měl hustotu $920\, \jd{kg\cdot m^{ - 3}}$, vzduch hustotu $1,2\, \jd{kg\cdot m^{ - 3}}$ a viskozitu $17,1 \cdot 10^{-7}\, \jd{Pa\cdot s}$. Užívali jsme elektrické pole o intenzitě $250\, \jd{kV\cdot m^{ - 1}}$.

Mějme elektrostatické pole neměnné v čase. Do toho pole vkládáme na stejné místo nabitou částici s nulovou počáteční rychlostí. Pečlivě sledujeme, jak se částice pohybuje, a zaznamenáváme si její trajektorii. A co nás překvapí – trajektorie částice nezávisí na její hmotnosti. Dokážete to vysvětlit?